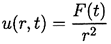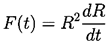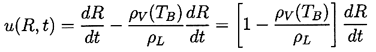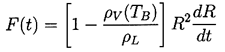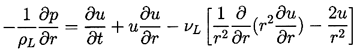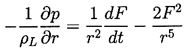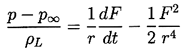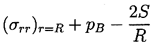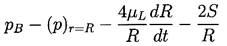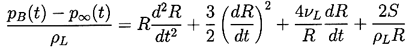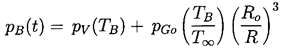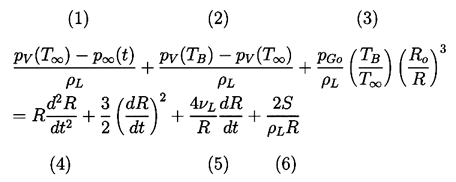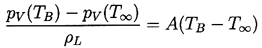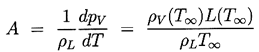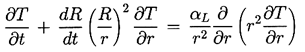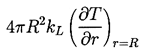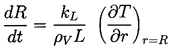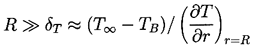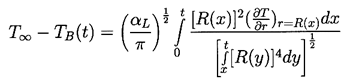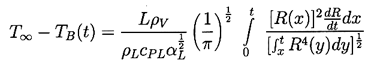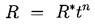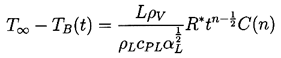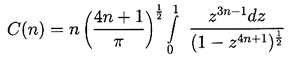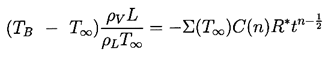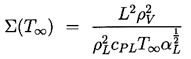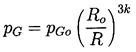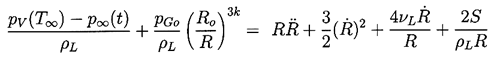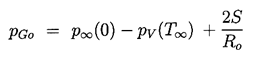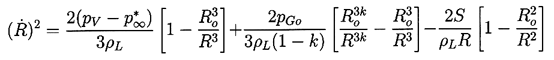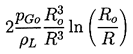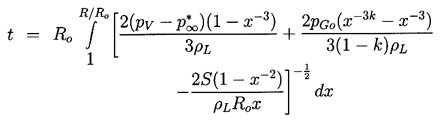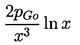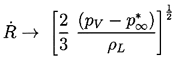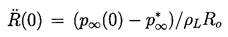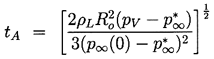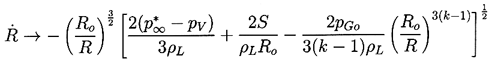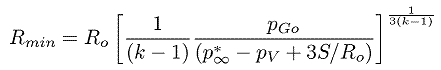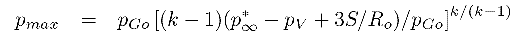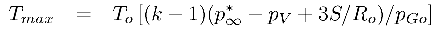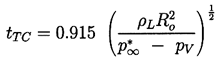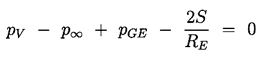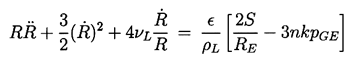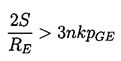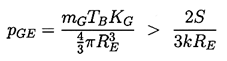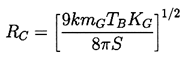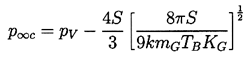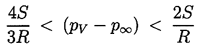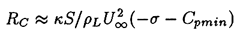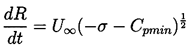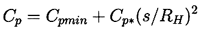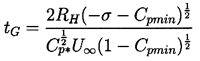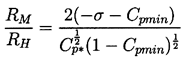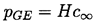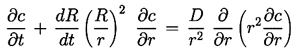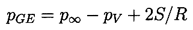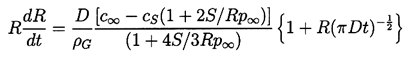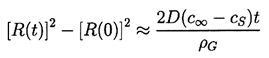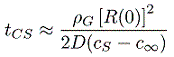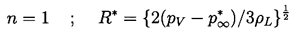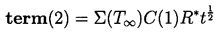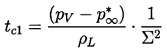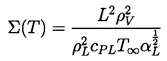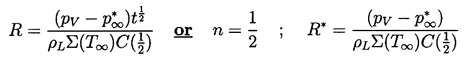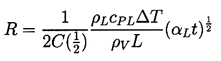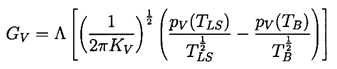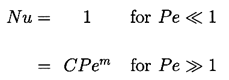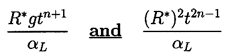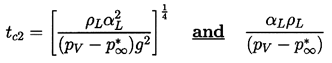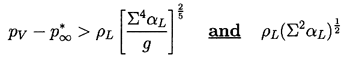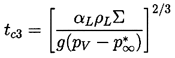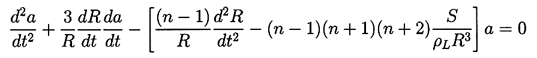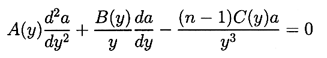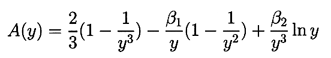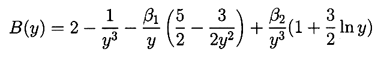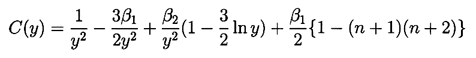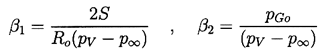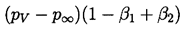CAVITATION AND BUBBLE DYNAMICS
by
Christopher Earls Brennen © Oxford University Press 1995
CHAPTER 2.
SPHERICAL BUBBLE DYNAMICS
2.1 INTRODUCTION
Having considered the initial formation of bubbles, we now proceed to
identify the subsequent dynamics of bubble growth and collapse.
The behavior of a single bubble in an infinite domain of liquid
at rest far from the bubble and with uniform temperature
far from the bubble will be examined first.
This spherically symmetric situation provides a simple case that is
amenable to analysis and reveals a number
of important phenomena.
Complications such as those introduced by the presence of nearby
solid boundaries will be discussed in the chapters which follow.
2.2 RAYLEIGH-PLESSET EQUATION
Consider a spherical bubble of radius,
R(t) (where t is time), in an infinite domain of liquid whose
temperature and pressure far from the bubble are T∞
and p∞(t) respectively.
The temperature, T∞ , is assumed to be a simple
constant since temperature gradients were eliminated a priori and
uniform heating of the liquid due to internal heat sources or
radiation will not be considered.
On the other hand, the pressure, p∞(t), is assumed to be
a known (and perhaps controlled) input which regulates the growth or
collapse of the bubble.
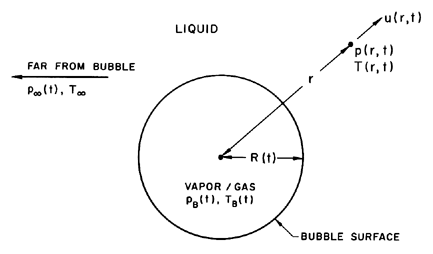
| Figure 2.1 Schematic of a spherical bubble in an
infinite liquid.
|
Though compressibility of the liquid can be important in the
context of bubble collapse, it will, for the present, be
assumed that the liquid density,
ρL , is a constant.
Furthermore, the dynamic viscosity, μL, is assumed
constant and uniform.
It will also be assumed that the contents of the bubble
are homogeneous and that the temperature,
TB(t), and pressure, pB(t), within the bubble are
always uniform.
These assumptions may not be justified in circumstances that will
be identified as the analysis proceeds.
The radius of the bubble, R(t),
will be one of the primary results of the analysis.
As indicated in Figure 2.1, radial position
within the
liquid will be denoted by the distance,
r, from the center of the bubble;
the pressure, p(r,t) , radial outward velocity, u(r,t), and
temperature, T(r,t),
within the liquid will be so designated.
Conservation of mass requires that
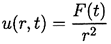 | ......(2.1)
|
|---|
where F(t) is related to R(t) by a kinematic boundary condition at the
bubble surface.
In the idealized case of zero mass transport across this interface,
it is clear that u(R,t)=dR/dt and hence
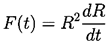 | ......(2.2)
|
|---|
But this is often a good approximation even when evaporation
or condensation is occurring at the interface.
To demonstrate this, consider a vapor bubble.
The volume rate of production of vapor must be equal to the
rate of increase of size of the bubble, 4πR2dR/dt,
and therefore the mass rate of evaporation must be
ρV(TB) 4πR2dR/dt where
ρV(TB) is the saturated vapor density at the
bubble temperature, TB.
This, in turn, must equal the mass flow of liquid inward relative
to the interface, and hence the inward velocity of liquid
relative to the interface is given by
ρV(TB)(dR/dt)/ρL.
Therefore
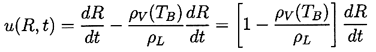 | ......(2.3)
|
|---|
and
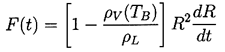 | ......(2.4)
|
|---|
In many practical cases
ρV(TB) « ρL
and therefore the approximate form of Equation 2.2 may be adequate.
For clarity we will continue with the approximate form
given in Equation 2.2.
Assuming a Newtonian liquid, the Navier-Stokes
equation for motion in the r direction,
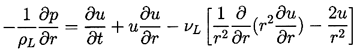 | ......(2.5)
|
|---|
yields, after substituting for u from u=F(t)/r2:
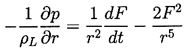 | ......(2.6)
|
|---|
Note that the viscous terms vanish; indeed, the only viscous contribution
to the Rayleigh-Plesset Equation 2.10 comes from the dynamic
boundary condition at the bubble surface.
Equation 2.6 can be integrated to give
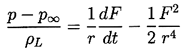 | ......(2.7)
|
|---|
after application of the condition
p→p∞ as r→∞.
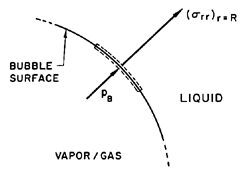
| Figure 2.2 Portion of the spherical bubble
surface.
|
To complete this part of the analysis, a dynamic
boundary condition on the bubble surface must be constructed.
For this purpose consider a control volume consisting of a small,
infinitely thin lamina containing a segment of interface (Figure 2.2).
The net force on this lamina in the radially outward direction
per unit area is
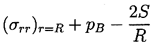 | ......(2.8)
|
|---|
or, since σrr=-p+2μL∂u/∂r,
the force per unit area is
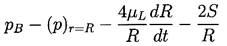 | ......(2.9)
|
|---|
In the absence of mass transport across the boundary
(evaporation or condensation) this force must be zero, and
substitution of the value for (p)r=R
from Equation (\ref{BE7}) with F=R2dR/dt
yields the generalized Rayleigh-Plesset equation
for bubble dynamics:
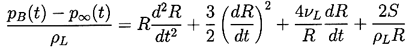 | ......(2.10)
|
|---|
Given p∞(t) this represents an equation that
can be solved to find R(t) provided pB(t)
is known. In the absence of the surface tension and viscous terms,
it was first derived and used by Rayleigh (1917). Plesset (1949)
first applied the equation to the problem of traveling cavitation
bubbles.
2.3 BUBBLE CONTENTS
In addition to the Rayleigh-Plesset equation, considerations
of the bubble contents are necessary.
To be fairly general,
it is assumed that the bubble contains some quantity of
contaminant gas whose partial pressure is pGo
at some reference size, Ro, and temperature, T∞ .
Then, if there is no appreciable mass transfer of gas to or from the liquid,
it follows that
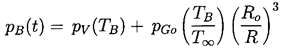 | ......(2.11)
|
|---|
In some cases this last assumption is not justified, and it
is necessary to solve a mass transport problem for the liquid
in a manner similar to that used for heat diffusion in the next
section (see Section 2.6).
It remains to determine TB(t).
This is not always necessary since, under some conditions, the
difference between the unknown TB and the known T∞
is negligible. But there are also circumstances in which the temperature
difference, (TB(t)-T∞), is important
and the effects
caused by this difference dominate the bubble dynamics. Clearly the
temperature difference,
(TB(t)-T∞), leads to a different vapor
pressure, pV(TB),
than would occur in the absence of such thermal effects, and this alters
the growth or collapse rate of the bubble. It is therefore instructive
to substitute Equation 2.11 into 2.10 and thereby write
the Rayleigh-Plesset equation in the following general form:
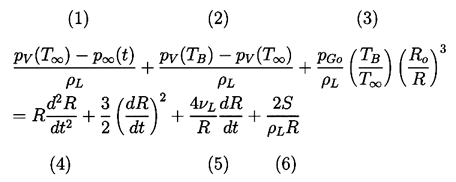 | ......(2.12)
|
|---|
The first term, (1), is the instantaneous tension or driving
term determined by the conditions far from the
bubble.
The second term, (2), will be referred to as the thermal term, and it will
be seen that very different bubble dynamics can be expected
depending on the magnitude of this term.
When the temperature difference is small, it is convenient to use a
Taylor expansion in which only the first derivative is retained to
evaluate
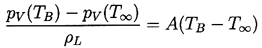 | ......(2.13)
|
|---|
where the quantity A may be evaluated from
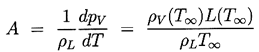 | ......(2.14)
|
|---|
using the Clausius-Clapeyron relation.
It is consistent with the Taylor
expansion approximation to evaluate ρV and L
at the known temperature T∞.
It follows that, for small temperature
differences, term (2) in Equation 2.12 is given by
A(TB-T∞).
The degree to which the bubble temperature, TB,
departs from the remote liquid temperature, T∞,
can have a major effect on the
bubble dynamics, and it is neccessary to discuss how this departure
might be evaluated. The determination
of (TB-T∞)
requires two steps. First, it requires
the solution of the heat diffusion equation,
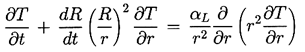 | ......(2.15)
|
|---|
to determine the temperature distribution,
T(r,t), within the liquid (αL is the thermal
diffusivity of the liquid).
Second, it requires an energy balance for the bubble.
The heat supplied to the interface from the liquid is
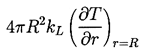 | ......(2.16)
|
|---|
where kL is the thermal conductivity of the liquid.
Assuming that all of this is used for vaporization of the liquid
(this neglects the heat used for heating or cooling the existing
bubble contents, which is negligible in many cases),
one can evaluate the mass rate of production of vapor and relate
it to the known rate of increase the volume of the bubble.
This yields
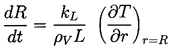 | ......(2.17)
|
|---|
where kL, ρV, L
should be evaluated at T=TB.
If, however, TB-T∞ is small, it is
consistent
with the linear analysis described earlier to evaluate these
properties at T=T∞.
The nature of the thermal effect problem is now clear.
The thermal term in the Rayleigh-Plesset Equation 2.12
requires a relation between (TB(t)-T∞)
and R(t).
The energy balance Equation 2.17 yields a relation between
(∂T/∂r)r=R and R(t).
The final relation between (∂T/∂r)r=R
and (TB(t)-T∞)
requires the solution of the heat diffusion equation.
It is this last step that causes considerable difficulty
due to the evident nonlinearities in the heat diffusion
equation; no exact analytic solution exists.
However, the solution of Plesset and Zwick (1952) provides a useful
approximation for many purposes.
This solution is confined to cases in which the thickness
of the thermal boundary layer,
δT, surrounding the bubble is small compared
with the radius of the bubble, a restriction that can be
roughly represented by the identity
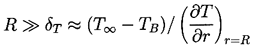 | ......(2.18)
|
|---|
The Plesset-Zwick result is that
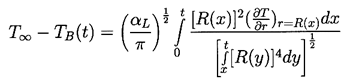 | ......(2.19)
|
|---|
where x and y are dummy time variables.
Using Equation 2.17 this can be written as
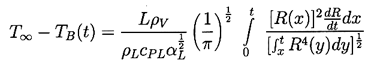 | ......(2.20)
|
|---|
This can be directly substituted
into the Rayleigh-Plesset equation to generate a complicated
integro-differential equation for R(t).
However, for present purposes it is more instructive to
confine our attention to regimes of bubble growth or collapse
that can be approximated by the relation
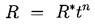 | ......(2.21)
|
|---|
where R* and n are constants. Then
the Equation 2.20 reduces to
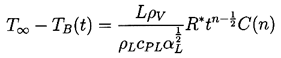 | ......(2.22)
|
|---|
where the constant
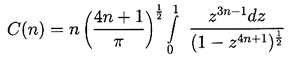 | ......(2.23)
|
|---|
and is of order unity for most values of n of
practical interest (0<n<1 in the case of bubble growth).
Under these conditions the linearized thermal term, (2), in the
Rayleigh-Plesset Equation 2.12 becomes
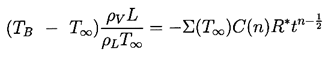 | ......(2.24)
|
|---|
where the thermodynamic parameter
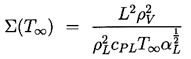 | ......(2.25)
|
|---|
It will be seen that this parameter,
Σ, whose units are m/sec3/2, is
crucially important in determining the bubble dynamic
behavior.
2.4 IN THE ABSENCE OF THERMAL EFFECTS
First we consider some of the characteristics
of bubble dynamics in the absence of any significant thermal effects.
This kind of bubble dynamic behavior is termed ``inertially controlled''
to distinguish it from the ``thermally controlled''
behavior discussed later.
Under these circumstances the temperature in the liquid is assumed uniform
and term (2) in the Rayleigh-Plesset Equation 2.12 is zero.
Furthermore, it will be assumed that the behavior of the gas in the bubble
is polytropic so that
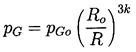 | ......(2.26)
|
|---|
where k is approximately constant.
Clearly k=1 implies a
constant bubble temperature and k=γ would model adiabatic
behavior. It should be understood that accurate evaluation of the
behavior of the gas in the bubble requires the solution of the
mass, momentum, and energy equations for the bubble contents combined
with appropriate boundary conditions which will include
a thermal boundary condition at the bubble wall. Such an analysis would
probably assume spherical symmetry. However, it is appropriate to
observe that any non-spherically symmetric internal motion would tend to
mix the contents and, perhaps,
improve the validity of the polytropic assumption.
With the above assumptions the
Rayleigh-Plesset equation becomes
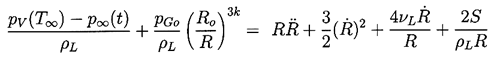 | ......(2.27)
|
|---|
where the overdot denotes d/dt.
Equation 2.27 without the viscous term was first derived and
used by Noltingk and Neppiras (1950, 1951); the viscous term was
investigated first by Poritsky (1952).
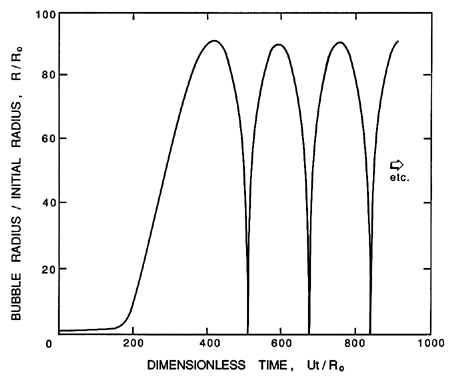
Figure 2.3
Typical solution of the Rayleigh-Plesset
equation for spherical bubble size/ initial size, R/R0.
The nucleus
enters a low-pressure region at a dimensionless time of 0 and is convected
back to the original pressure at a dimensionless time of 500.
The low-pressure region is sinusoidal and symmetric about 250.
Equation 2.27 can be readily integrated numerically to find R(t) given
the input p∞(t), the temperature T∞,
and the other constants.
Initial conditions are also required and, in the context of
cavitating flows, it is appropriate to assume that the
microbubble of radius Ro is in
equilibrium at t=0 in the fluid at a pressure
p∞(0) so that
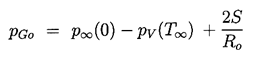 | ......(2.28)
|
|---|
and that (dR/dt)t=0=0.
A typical solution for Equation 2.27 under these conditions and with
a pressure p∞(t), which first decreases below
p∞(0) and
then recovers to its original value, is shown in Figure 2.3.
The general features of this solution are characteristic of
the response of a bubble as it passes through any low-pressure
region; they also reflect the strong nonlinearity of Equation 2.27.
The growth is fairly smooth and the maximum size occurs after
the minimum pressure.
The collapse process is quite different.
The bubble collapses catastrophically, and this is followed
by successive rebounds and collapses.
In the absence of dissipation mechanisms such as viscosity these rebounds
would continue indefinitely without attenuation.
Analytic solutions to Equation 2.27 are limited to the case
of a step function change in p∞.
Nevertheless, these solutions reveal some of the characteristics of
more general pressure histories, p∞(t),
and are therefore valuable to document.
Denoting the constant value of
p∞(t>0) by
p∞*,
Equation 2.27 can be integrated by
multiplying through by
2R2dR/dt and forming time derivatives.
Only the viscous term cannot be integrated in this way, and
what follows is confined to the inviscid case.
After integration, application of the initial condition
(dR/dt)t=0=0 yields
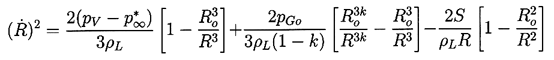 | ......(2.29)
|
|---|
where, in the case of isothermal gas behavior, the term involving
pGo becomes
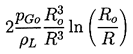 | ......(2.30)
|
|---|
By rearranging Equation 2.29 it follows that
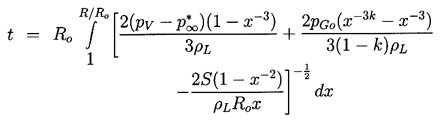 | ......(2.31)
|
|---|
where, in the case k=1, the gas term is replaced by
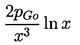 | ......(2.32)
|
|---|
This integral can be evaluated numerically to find R(t),
albeit indirectly.
Consider first the characteristic behavior for bubble
growth which this solution exhibits when
p∞*<p∞(0).
Equation 2.29 shows that the asymptotic growth rate for
R»Ro is given by
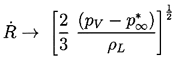 | ......(2.33)
|
|---|
Hence, following an initial period of acceleration, whose duration,
tA, may be estimated from this relation and the value of
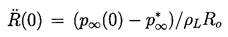 | ......(2.34)
|
|---|
to be
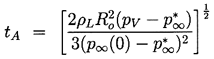 | ......(2.35)
|
|---|
the subsequent velocity of the interface is relatively
constant. It should be emphasized that Equation 2.33 nevertheless
represents explosive growth of the bubble, in which the volume
displacement is increasing like t3.
Now contrast the behavior of a bubble caused to collapse by
an increase in p∞ to
p*∞.
In this case when R«Ro Equation 2.29 yields
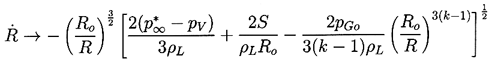 | ......(2.36)
|
|---|
where, in the case of k=1, the gas term is replaced by
2pGoln(Ro/R)/ρL.
However, most bubble collapse motions
become so rapid that the gas behavior is much closer to adiabatic
than isothermal, and we will therefore assume k is not equal to 1.
For a bubble with a substantial gas content the asymptotic
collapse velocity given by Equation 2.36
will not be reached and the bubble will simply oscillate
about a new, but smaller, equilibrium radius. On the other hand, when
the bubble contains very little gas,
the inward velocity will continually increase (like
R-3/2) until the last term within the
square brackets reaches a magnitude comparable with the other terms.
The collapse velocity will then decrease and a
minimum size given by
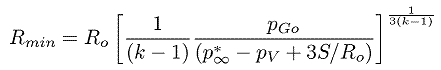 | ......(2.37)
|
|---|
will be reached, following which the bubble will rebound.
Note that, if pGo is small, the
Rmin could be very
small indeed. The pressure and temperature of the gas in the bubble
at the minimum radius are then given by pmax and
Tmax where
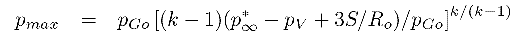 | ......(2.38)
|
|---|
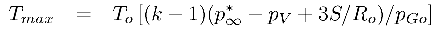 | ......(2.39)
|
|---|
We will comment later on the magnitudes of these temperatures and
pressures (see Section 3.2).
The case of zero gas content presents a special albeit
somewhat hypothetical problem, since apparently the
bubble will reach zero size and at that time have an
infinite inward velocity. In the absence of
both surface tension and gas content,
Rayleigh (1917) was able
to integrate Equation 2.31 to obtain
the time, tTC, required for total collapse from
R=Ro to
R=0:
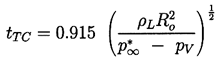 | ......(2.40)
|
|---|
It is important at this point to emphasize that while the above results
for bubble growth are quite practical, the results for bubble collapse may be
quite misleading. Apart from the neglect of thermal effects, the analysis
was based on two other assumptions that may be violated during collapse.
Later we shall see that the final stages of collapse may involve such high
velocities (and pressures) that the assumption of liquid incompressibility
is no longer appropriate. But, perhaps more important, it transpires
(see Chapter 5) that a collapsing bubble loses its spherical
symmetry in ways that can have important engineering consequences.
2.5 STABILITY OF VAPOR/GAS BUBBLES
Apart from the characteristic bubble growth and collapse
processes discussed in the last section, it is also important to
recognize that the equilibrium condition
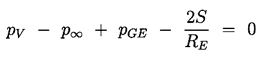 | ......(2.41)
|
|---|
may not always represent a stable equilibrium state at
R=RE with a partial pressure of gas pGE.
Consider a small perturbation in the size of the bubble
from R=RE to R=RE(1+ε),
ε«1
and the response resulting from the Rayleigh-Plesset
equation.
Care must be taken to distinguish two possible cases:
-
The partial pressure of the gas remains the same at pGE.
-
The mass of gas in the bubble and its temperature, TB,
remain the same.
From a practical point of view the Case (i) perturbation is
generated over a length of time sufficient to allow adequate mass
diffusion in the liquid so that the partial pressure of
gas is maintained at the value appropriate to the concentration
of gas dissolved in the liquid.
On the other hand, Case (ii) is considered to take place too rapidly
for significant gas diffusion.
It follows that in Case (i) the gas term in the Rayleigh-Plesset
Equation 2.27 is pGE/ρL whereas in
Case (ii) it is
pGERE3k/ρLR3k.
If n is defined as zero for Case (i) and n=1 for Case (ii)
then substitution of R=RE(1+ε) into the
Rayleigh-Plesset equation yields
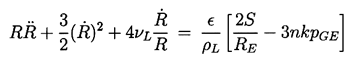 | ......(2.42)
|
|---|
Note that the right-hand side has the same sign as ε if
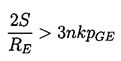 | ......(2.43)
|
|---|
and a different sign if the reverse holds.
Therefore, if the above inequality holds, the left-hand side of
Equation 2.42 implies that the velocity and/or acceleration
of the bubble radius has the same sign as the perturbation, and
hence the equilibrium is unstable
since the resulting motion will cause the bubble to deviate
further from R=RE. On the other hand, the equilibrium
is stable if npGE>2S/3RE.
First consider Case (i) which must always be
unstable since the inequality 2.43 always holds if n=0.
This is simply a restatement of the fact (discussed in
Section 2.6)
that, if one allows time for mass diffusion, then all bubbles
will either grow or shrink indefinitely.
Case (ii) is more interesting since in many of the practical
engineering situations pressure levels change over a period of
time that is short compared with the time required for
significant gas diffusion.
In this case a bubble in stable equilibrium requires
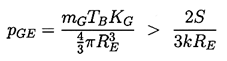 | ......(2.44)
|
|---|
where mG is the mass of gas in the bubble and KG
is the gas constant. Indeed for a given
mass of gas there exists a critical
bubble size, RC, where
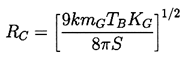 | ......(2.45)
|
|---|
This critical radius was first identified by Blake (1949) and Neppiras
and Noltingk (1951) and is often referred to as the
Blake critical
radius. All bubbles of radius RE<RC can exist in
stable equilibrium, whereas all bubbles of radius
RE>RC must be unstable.
This critical size could be reached by decreasing the ambient pressure from
p∞ to the critical value, p∞c,
where from Equations 2.45 and 2.41 it follows that
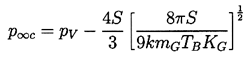 | ......(2.46)
|
|---|
which is often called the Blake threshold pressure.
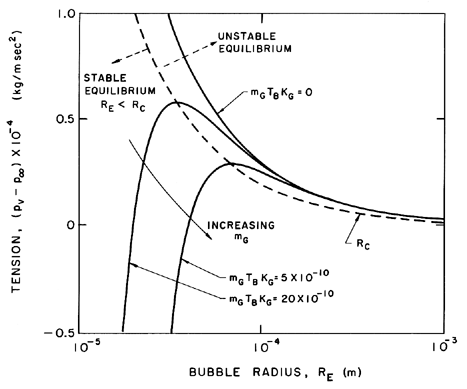
Figure 2.4
Stable and unstable bubble equilibrium radii as a function
of the tension for various masses of gas in the bubble. Stable and
unstable conditions are separated by the dotted line. Adapted from
Daily and Johnson (1956).
The isothermal case (k=1) is presented graphically in Figure 2.4
where the solid lines represent equilibrium conditions for a
bubble of size RE plotted against the tension
(pV -p∞)
for various fixed masses of gas in the bubble and a fixed
surface tension. The critical radius for any particular
mG corresponds to the maximum in each curve.
The locus of the peaks is the graph of RC values and is
shown by the dashed line whose equation is
(pV -p∞)=4S/3RE.
The region to the right of the dashed line represents unstable
equilibrium conditions.
This graphical representation was used by Daily and Johnson (1956)
and is useful in visualizing the quasistatic
response of a bubble when subjected to a decreasing pressure.
Starting in the fourth quadrant under conditions in which the
ambient pressure p∞>pV,
and assuming the mass of gas
in the bubble is constant, the radius RE will first
increase as (pV -p∞) increases.
The bubble will pass through a series of stable equilibrium
states until the particular critical pressure corresponding to the
maximum is reached. Any slight decrease in
p∞ below the value corresponding to
this point will result in explosive cavitation growth regardless
of whether p∞ is further decreased or not.
Indeed, it is clear from this analysis that the critical tension
for a liquid should be given by 4S/3R rather than 2S/R
as maintained in Chapter 1, since stable equilibrium
conditions do not exist in the range
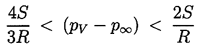 | ......(2.47)
|
|---|
Other questions arise from inspection of Figure 2.4.
Note that for a given subcritical tension two alternate
equilibrium states exist, one smaller stable state and one
larger unstable state.
Suppose that a bubble at the smaller stable state is also
subjected to pressure oscillations of sufficient magnitude
to cause the bubble to momentarily exceed the size, RC.
It would then grow explosively without bound.
This effect is important in understanding the
role of turbulence in cavitation inception or the response of a
liquid to an acoustic field (see Chapter 4).
This stability phenomenon has important consequences in many cavitating
flows. To recognize this, one must visualize a spectrum of sizes of
cavitation nuclei being convected into a region of low pressure
within the flow. Then the p∞ in
Equations 2.41 and 2.47 will be the local pressure in the liquid
surrounding the
bubble, and p∞ must be less than pV for
explosive cavitation
growth to occur. It is clear from the above analysis that all of the nuclei
whose size, R, is greater than some critical value will become unstable,
grow explosively, and cavitate, whereas those nuclei smaller than that
critical size will react passively and will therefore not become visible
to the eye. Though the actual response of the bubble is dynamic and
p∞ is changing continuously, we can nevertheless anticipate
that the crtical nuclei size will be given approximately by
4S/3(pV -p∞)* where
(pV -p∞)* is some
representative measure of the tension in the low-pressure region.
Note that the lower the pressure level, p∞,
the smaller the
critical size and the larger the number of nuclei that are activated.
This accounts for the increase in the number of bubbles observed in
a cavitating flow as the pressure is reduced.
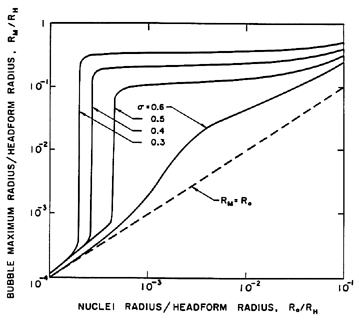
|
Figure 2.5
The maximum size, RM , to which a cavitation bubble grows
according to the Rayleigh-Plesset equation as a function of the
original nucleus size, Ro, and the cavitation number, σ, in
the flow around an axisymmetric headform of radius, RH , with
Weber number,
ρLRHU∞2/S=28000
(from Ceccio and Brennen 1991).
A quantitative example of this effect is shown in Figure 2.5, which
presents results from the integration of the Rayleigh-Plesset equation
for bubbles in the flow around an axisymmetric headform.
It shows the maximum size which the bubbles achieve as a function of the
size of the original nucleus for a typical Weber number,
ρLRHU∞2/S, of 28000
where U∞ and RH are
the free stream velocity
and headform radius. Data are plotted for four different cavitation numbers,
σ, representing different ambient pressure levels. Note that the
curves for σ<0.5 all have abrupt vertical sections at certain
critical nuclei sizes and that this critical size decreases with decreasing
σ. Numerical results for this and other flows show that the
critical size, RC, adheres fairly closely to the nondimensional
version of the expression derived earlier,
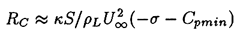 | ......(2.48)
|
|---|
where Cpmin is the minimum pressure coefficient in the flow
and the factor κ is close to unity.
Note also from Figure 2.5 that, whatever their initial size, all
unstable nuclei grow to roughly the same maximum size. This is because
both the asymptotic growth rate and the time available for growth are
relatively independent of the size of the original nucleus. From
Equation 2.33 the growth rate is given approximately by
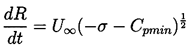 | ......(2.49)
|
|---|
Moreover, if the pressure near the minimum pressure point is represented
by
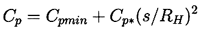 | ......(2.50)
|
|---|
where s is a coordinate measured along the surface,
RH is the typical dimension of the body, and
Cp* is a constant which is typically of
order one, then the typical time available for growth, tG, is
given approximately by
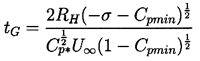 | ......(2.51)
|
|---|
It follows that the maximum size, RM, will be given roughly
by
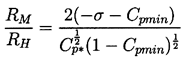 | ......(2.52)
|
|---|
and therefore only changes modestly with cavitation number within
the range of significance.
2.6 GROWTH BY MASS DIFFUSION
In most of the circumstances considered in this chapter, it is assumed
that the events occur too rapidly for significant mass transfer of
contaminant gas to occur between the bubble and the liquid. Thus we
assumed in Section 2.3 and elsewhere that the mass of contaminant gas
in the bubble remained constant. It is convenient to reconsider this issue
at this point, for the methods of analysis of mass diffusion will clearly
be similar to those of thermal diffusion (Scriven 1959). Moreover, there
are some issues that require analysis of the rate of increase or decrease
of the mass of gas in the bubble. One of the most basic issues is the fact
that any and all of the gas-filled microbubbles that are present in
a subsaturated liquid (and particularly in water) should dissolve away
if the ambient pressure is sufficiently high. Henry's law states that
the partial pressure of gas, pGE, in the bubble,
which is in equilibrium with a saturated concentration,
c∞, of gas dissolved in the
liquid will be given by
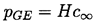 | ......(2.53)
|
|---|
where H is Henry's law constant for that gas and liquid combination.
(Note that H decreases substantially with temperature.) Consequently,
if the ambient pressure, p∞, is greater than
(Hc∞+pV -2S/R), the bubble should dissolve
away completely.
As we discussed in Section 1.12, experience is
contrary to this theory, and microbubbles persist even when the
liquid is subjected to several atmospheres of pressure for an extended period.
The process of mass transfer can be analysed by noting that the
concentration, c(r,t), of gas in the liquid will be governed by a
diffusion equation identical in form to Equation 2.15,
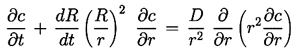 | ......(2.54)
|
|---|
where D is the mass diffusivity, typically
2×10-5cm2/sec for air in water at
normal temperatures. As Plesset and
Prosperetti (1977) demonstrate, the typical bubble growth rates due to
mass diffusion are so slow that the convection term (the second term on
the left-hand side of Equation 2.54) is negligible.
The simplest problem is that of a bubble of radius, R, in a liquid
at a fixed ambient pressure, p∞, and gas concentration,
c∞.
In the absence of inertial effects the partial pressure of gas in the bubble
will be pGE where
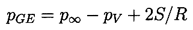 | ......(2.55)
|
|---|
and therefore the concentration of gas at the liquid interface is
cS=pGE/H. Epstein and Plesset (1950) found an
approximate solution to the problem of a bubble in a liquid initially at
uniform gas concentration, c∞, at time, t=0, which
takes the form
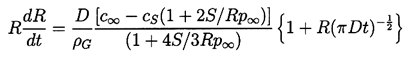 | ......(2.56)
|
|---|
where ρG is the density of gas in the bubble and
cS is the
saturated concentration at the interface at the partial pressure given
by Equation 2.55 (the vapor pressure is neglected in their
analysis). The last term
in Equation 2.56, R(πDt)-½, arises
from a growing diffusion boundary layer in the liquid
at the bubble surface. This layer grows like (Dt)½.
When t is large, the last term in Equation 2.56
becomes small and the characteristic growth
is given approximately by
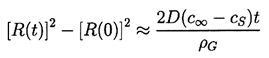 | ......(2.57)
|
|---|
where, for simplicity, we have neglected surface tension.
It is instructive to evaluate the typical duration of growth (or shrinkage).
From Equation 2.57 the time required for complete solution
is tCS where
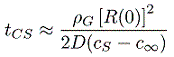 | ......(2.58)
|
|---|
Typical values of (cS-c∞)/ρG
of 0.01 (Plesset and Prosperetti 1977) coupled with
the value of D given above lead to complete solution of
a 10μm bubble in about 2.5s. Though short, this is a long
time by the standards of most bubble dynamic phenomena.
The fact that a microbubble should dissolve within seconds
leaves unresolved the question of why cavitation nuclei persist
indefinitely. One possible explanation is that the interface is
immobilized by the effects of surface contamination.
Another is that the bubble is
imbedded in a solid particle in a way that inhibits the solution
of the gas, the so-called Harvey nucleus. These issues were discussed
previously in Section 1.12.
Finally we note that there is an important mass diffusion effect
caused by ambient pressure oscillations in
which nonlinearities can lead to bubble growth even in a subsaturated
liquid. This is known as ``rectified diffusion''
and is discussed later in Section 4.9.
2.7 THERMAL EFFECTS ON GROWTH
In Sections 2.4 through 2.6 some of the characteristics
of bubble dynamics in the absence of thermal effects were
explored.
It is now necessary to examine the regime of validity of
these analyses, and it is convenient to first evaluate the
magnitude of the thermal term 2.24 which was neglected in
Equation 2.12 in order to produce Equation 2.27.
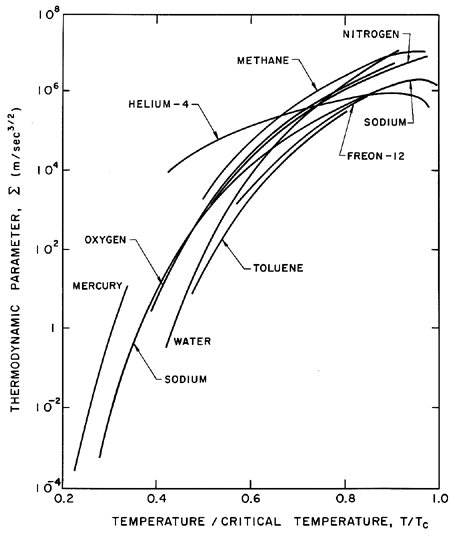
| Figure 2.6
Values of the thermodynamic parameter,
Σ, for various saturated liquids as a function of the reduced
temperature, T/TC.
|
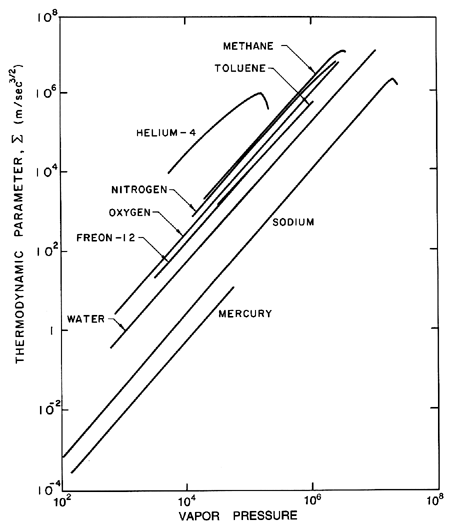
| Figure 2.7
Values of the thermodynamic parameter,
Σ, for various saturated liquids as a function of the vapor
pressure (in kg/m s2).
|
First examine the case of bubble growth.
The asymptotic growth rate given by Equation 2.33 is
constant and hence in the characteristic case of a constant
p∞, terms (1), (3), (4), (5), and (6) in
Equation 2.12 are all either constant or
diminishing in magnitude as time progresses.
Furthermore, a constant, asymptotic growth rate corresponds to the case
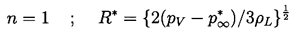 | ......(2.59)
|
|---|
in Equation 2.21.
Consequently, according to Equation 2.24, the thermal term
(2) in its linearized form for small
(T∞-TB)
will be given by
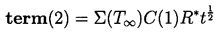 | ......(2.60)
|
|---|
Under these conditions, even if the thermal term is initially
negligible, it will gain in magnitude relative to all the
other terms and will ultimately affect the growth
in a major way.
Parenthetically it should be added that the Plesset-Zwick
assumption of a small thermal boundary layer thickness,
δT, relative
to R can be shown to hold throughout the inertially
controlled growth period since δT increases
like (αLt)½
whereas R is increasing
linearly with t.
Only under circumstances of very slow growth might the
assumption be violated.
Using the relation 2.60, one can define
a critical time, tc1 (called the
first critical time), during the growth when the order of
magnitude of term (2) becomes equal to the order of
magnitude of the retained terms, as represented by
(dR/dt)2.
This first critical time is given by
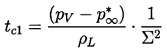 | ......(2.61)
|
|---|
where the constants of order unity have been omitted for clarity.
Thus tc1 depends not only on the tension
(pV -p∞*)/ρL
but also on
Σ(T∞), a purely thermophysical
quantity that is a function only of the liquid temperature.
Recalling Equation 2.25,
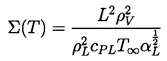 | ......(2.62)
|
|---|
it can be anticipated that Σ2
will change by many, many
orders of magnitude in a given liquid as
the temperature T∞ is varied from the triple point to the
critical point since Σ2
is proportional to (ρV/ρL)4.
As a result the critical time, tc1, will vary by many
orders of magnitude.
Some values of Σ for a number of liquids are
plotted in Figure 2.6 as a function of the reduced
temperature T/TC and in Figure 2.7 as a function of the
vapor pressure. As an example, consider a typical cavitating flow
experiment in a water tunnel with a tension of the order of
104 kg/m s2. Since water at 20°C has a value
of Σ
of about 1 m/s3/2, the first critical time is
of the order of 10s, which is very much longer than the time
of growth of bubbles.
Hence the bubble growth occurring in this case is unhindered by
thermal effects; it is ``inertially controlled" growth.
If, on the other hand, the tunnel water were heated to 100°C
or, equivalently, one
observed bubble growth in a pot of boiling water at superheat of
2°K, then since Σ is approximately
103 m/s3/2 at 100°C
the first critical time would be 10μs.
Thus virtually all the bubble growth observed would be
``thermally controlled."
2.8 THERMALLY CONTROLLED GROWTH
When the first critical time is exceeded it is clear that the
relative importance of the various terms in the Rayleigh-Plesset Equation,
2.12, will change.
The most important terms become the driving term (1)
and the thermal term (2) whose magnitude is much larger
than that of the inertial terms (4).
Hence if the tension (pV -p∞*)
remains constant, then the solution using the form of Equation 2.24
for the thermal term must have n=½ and the asymptotic
behavior is
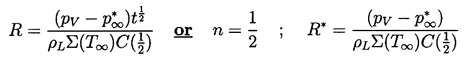 | ......(2.63)
|
|---|
Consequently, as time proceeds, the inertial, viscous, gaseous, and surface
tension terms in the Rayleigh-Plesset equation
all rapidly decline in importance.
In terms of the superheat, ΔT, rather than the tension
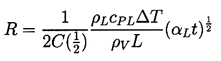 | ......(2.64)
|
|---|
where the group
ρLcPLΔT/ρVL
is termed the Jakob Number in the
context of pool boiling and
ΔT=TW -T∞,
TW being the wall temperature.
The result, Equation 2.63, demonstrates that the rate of growth of the
bubble decreases substantially after the first critical
time, tc1, is reached and that R subsequently increases like
t½ instead of t.
Moreover, since the thermal boundary layer also increases
like (αLt)½,
the Plesset-Zwick assumption remains valid indefinitely.
An example of this thermally inhibited bubble growth is including in
Figure 2.8, which is taken from Dergarabedian (1953).
We observe that the
experimental data and calculations using the Plesset-Zwick method agree
quite well.
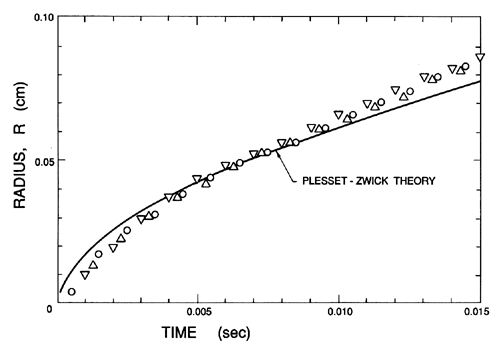
| Figure 2.8
Experimental observations of the growth of
three vapor bubbles (three different symbols) in
superheated water at 103.1°C compared with the growth expected using
the Plesset-Zwick theory (adapted from Dergarabedian 1953).
|
When bubble growth is caused by decompression so that
p∞(t)
changes substantially with time during growth, the simple approximate
solution of Equation 2.63 no longer holds and the analysis of the unsteady
thermal boundary layer surrounding the bubble becomes considerably
more complex. One must then solve the diffusion Equation 2.15,
the energy equation (usually in the approximate form of Equation
2.17) and the Rayleigh-Plesset Equation 2.12 simultaneously,
though for the thermally controlled growth being considered here, most
of the terms in Equation 2.12 become negligible so that the
simplification, pV(TB)=p∞(t),
is usually justified.
When p∞ is a constant this reduces to the problem
treated by
Plesset and Zwick (1952) and later addressed by Forster and Zuber (1954)
and Scriven (1959). Several different approximate solutions to the general
problem of thermally controlled bubble growth during liquid decompression
have been put forward by Theofanous et al. (1969), Jones and
Zuber (1978) and Cha and Henry (1981). Theofanous et al. include
nonequilibrium thermodynamic effects
on which we comment in the following section. If
these are ignored, then all three analyses yield qualitatively similar
results which also agree quite well with the experimental data of
Hewitt and Parker (1968) for bubble growth in liquid nitrogen.
Figure 2.9 presents a typical example of the data of Hewitt
and Parker and a comparison with the three analytical treatments
mentioned above.
Several other factors can complicate and alter the dynamics
of thermally controlled growth, and these are discussed in the sections
which follow. Nonequilibrium effects are addressed in
Section 2.9.
More important are the modifications to the heat transfer mechanisms at
the bubble surface that can be caused by surface instabilities or by
convective heat transfer. These are reviewed in Sections
2.10 and 2.12.
2.9 NONEQUILIBRIUM EFFECTS
One factor that could affect the dynamics
of thermally controlled growth is whether or not the liquid at the
interface is in thermal equilibrium with the vapor in the bubble.
Most of the analyses assume that the temperature of the liquid
at the interface, TLS, is the temperature of the saturated
vapor in the bubble, TB . Theofanous et al. (1969) have
suggested that this might not be the case because of the high
evaporation rate. They employ an
accommodation coefficient, Λ,
defined (Schrage 1953) by
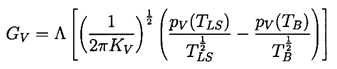 | ......(2.65)
|
|---|
where GV is the evaporative mass flux and KV is the
gas constant of the vapor. For a chosen value of Λ this
effectively defines a temperature discontinuity at the interface.
Clearly Λ=∞ corresponds to the previously assumed equilibrium
condition. Plesset and Prosperetti (1977) demonstrate that if Λ is of
order unity then the nonequilibrium correction is of the order of the
Mach number of the bubble wall motion and is therefore negligible
except, perhaps, near the end of a violent bubble collapse (see Fujikawa
and Akamatsu 1980 and Section 3.2). On the other
hand, if Λ is much smaller than unity, significant nonequilibrium
effects might be encountered.
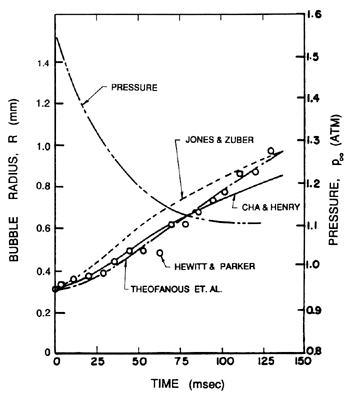
| Figure 2.9
Data from Hewitt and Parker (1968) on the growth of a vapor
bubble in liquid nitrogen (pressure/time history also shown) and
comparison with the analytical treatments by Theofanous et al.
(1969), Jones and Zuber (1978), and Cha and Henry (1981).
|
Theofanous et al. (1969) explore the effects of small values of
Λ theoretically. They confirm that values of order unity do
not yield bubble
histories that differ by very much from those that assume equilibrium.
Values of Λ of the order of 0.01 did produce substantial differences.
However, the results using equilibrium appear to compare favorably with
the experimental results as shown in Figure 2.9. This suggests that
nonequilibrium effects have little effect on thermally controlled
bubble growth though the issue is not entirely settled since some
studies do suggest that values of Λ as low as 0.01 may be possible.
2.10 CONVECTIVE EFFECTS
Another way in which the rate of heat transfer to the interface
may be changed is by convection caused by relative motion between
the bubble and the liquid.
Such enhancement of the heat transfer rate is normally represented
by a Nusselt number, Nu,
defined as the ratio of the actual
heat transfer rate divided by the rate of heat transfer by conduction.
Therefore in the present context the factor, Nu, should be included
as a multiplier in the thermal term of the Rayleigh-Plesset equation.
Then one seeks a relationship between Nu and the
Peclet number, Pe=WR/αL, where W is the
typical translational velocity of the bubble
relative to the liquid.
The appropriate relationship for a growing and translating bubble
is not known; analytically this represents a problem that
is substantially more complex than that tackled by Plesset and Zwick.
Nevertheless, it is of interest to speculate on the form of
Nu(Pe) and observe the consequences for the bubble growth rate.
Therefore let us assume that this relationship takes the
approximate form common
in many convective heat transfer problems:
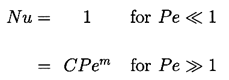 | ......(2.66)
|
|---|
where C is some constant of order unity.
We must also decide on the form of the relative velocity,
W, which could have several causes.
In either a cavitating flow or in pool boiling it could be
due to pressure gradients within the liquid due to acceleration of
the liquid.
It could also be caused by the presence of nearby solid boundaries.
Despite the difficulties of accurate assessment of
the convective heat transfer effects, let us consider the qualitative
effects of two possible translational motions on a bubble growing
like R=R*tn. The first effect is that
due to buoyancy; the relative velocity,
W, caused by buoyancy in the absence of viscous drag
will be given approximately by gt. The viscous
drag on the bubble will have little effect so long as
νLt « R2.
The second example is a bubble growing on a solid wall
where the effective convective velocity is roughly given
by dR/dt and hence
W is proportional to R*tn-1.
Thus the Peclet numbers for the two cases are respectively
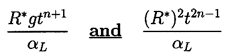 | ......(2.67)
|
|---|
Consider first the case of inertially controlled growth for which
n=1. Then it follows that convective heat transfer effects
will only occur
for Pe≥1 or for times t>tc2 where
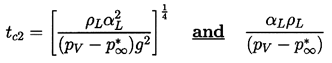 | ......(2.68)
|
|---|
respectively where the asymptotic growth rate given by Equation 2.33
has been used. Consequently,
the convective enhancement of the heat transfer will only
occur during the inertially controlled growth
if tc2<tc1 and this requires that
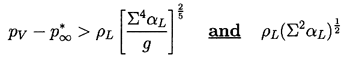 | ......(2.69)
|
|---|
respectively. Since Σ increases rapidly with temperature
it is much
more likely that these inequalities will be true at
low reduced temperatures
than at high reduced temperatures.
For example, in water at 20°C the
right-hand sides of Inequality 2.69 are respectively
30 and 4 kg/m sec2, very small tensions (and correspondingly
minute superheats) that could readily occur.
If the tension is larger than this critical value,
then convective effects would become important.
On the other hand, in water at 100°C the values are respectively
equivalent to superheats of 160°K and 0.5°K,
which are less likely to occur.
It follows that in each of the two bubble motions assumed
there is some temperature below which one would
expect Pe to reach unity prior to tc1.
The question is what happens thereafter, for clearly the thermal
effect that would otherwise begin at tc1 is now going to be
altered by the enhanced heat transfer.
When Pe>1 the thermal term in the Rayleigh-Plesset equation
will no longer grow like t½ but will increase like
t½/Nu which, according to the relations
2.67, is like t½-2m
and t½-m for the two bubble motions.
If, as in many convective heat transfer problems, m=½,
it would follow that thermal inhibition of the growth would be
eliminated and the inertially controlled growth would
continue indefinitely.
Finally, consider the other possible scenario in which
convective heat transfer effects might
influence the thermally controlled growth in the event that
tc2>tc1. Given n=½, the Peclet
number for buoyancy-induced motion would
become unity at
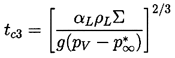 | ......(2.70)
|
|---|
using Equation 2.63. Consequently,
convective heat transfer could alter the form of the thermally controlled
growth after t=tc3; indeed, it is possible that inertially controlled
growth could resume after tc3 if m>¼.
In the other example of bubble growth at a wall, the Peclet number
would remain at the value less than unity which it had attained
at tc1.
Consequently, the
convective heat transfer effects would delay the onset
of thermally inhibited growth indefinitely if
(pV -p∞*) » ρL
(Σ2αL)½
but would have little or no effect on either the onset
or form of the thermally controlled growth if the reverse
were true.
2.11 SURFACE ROUGHENING EFFECTS
Another important phenomenon that can affect the heat transfer process
at the interface during bubble growth (and therefore affect the bubble
growth rate) is the development of an instability on the interface. If
the bubble surface becomes rough and turbulent, the increase in
the effective surface area and the
unsteady motions of the liquid near that surface can lead to a
substantial enhancement of the rate of heat transfer to the interface.
The effect is to delay (perhaps even indefinitely) the
point at which the rate of growth is altered by thermal effects.
This is one possible
explanation for the phenomenon of vapor explosions which are essentially
the result of an extended period of inertially controlled bubble growth.
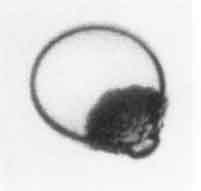
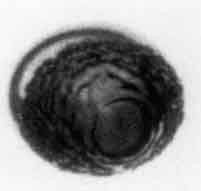
Figure 2.10
Typical photographs of a rapidly growing bubble in a droplet of
superheated ether suspended in glycerine. The bubble is the dark,
rough mass; the droplet is clear and transparent. The photographs, which
are of different events, were taken 31, 44, and 58μs after nucleation
and the droplets are approximately 2mm in diameter. Reproduced from
Frost and Sturtevant (1986) with the permission of the authors.
Shepherd and Sturtevant (1982) and Frost and Sturtevant (1986) have
examined rapidly growing nucleation bubbles near the limit of superheat
and have found growth rates substantially
larger than expected when the bubble was in the thermally controlled growth
phase. The experiments examined bubble growth within droplets of
superheated liquid suspended in another immiscible liquid.
Typical photographs are shown in Figure 2.10 and reveal that
the surfaces of the bubbles are rough and irregular. The enhancement
of the heat transfer caused by this roughening is probably responsible
for the larger growth rates.
Shepherd and Sturtevant (1982) attribute the roughness to the development
of a baroclinic interfacial instability similar to the Landau-Darrieus
instability of flame fronts.
It is also of interest to note that Frost and Sturtevant report that
the instability could be suppressed by increasing the ambient pressure
and therefore the temperature and density within the bubble. At an
ambient pressure of 2bar, the onset of the instability could be observed
on the surface of ether bubbles and was accompanied by a jump in the
radiated pressure associated with the sudden acceleration in the
growth rate. At higher ambient pressures the instability could be
completely suppressed.
This occurs because the growth rate of the instability increases with
the rate of growth of the bubble, and both are significantly reduced
at the higher ambient pressures. It may be that, under other circumstances,
the Rayleigh-Taylor
instabilities described in Section 2.12 could
give rise to a similar effect.
2.12 NONSPHERICAL PERTURBATIONS
Apart from the phenomena described in the preceding section, it has,
thus far, been tacitly assumed that the bubble remains
spherical during the growth or collapse process;
in other words, it has been assumed that the bubble is stable
to nonspherical distortions. There are, however,
circumstances in which this is not true, and the subsequent
departure from a smooth spherical shape can have important
practical consequences.
The stability to nonspherical disturbances has been investigated
from a purely hydrodynamic point of view by Birkhoff (1954) and
Plesset and Mitchell (1956), among others.
These analyses essentially examine the spherical equivalent
of the Rayleigh-Taylor instability;
they do not include thermal effects.
If the inertia of the gas in the bubble is assumed to
be negligible, then the amplitude, a(t), of a
spherical harmonic distortion of order n
(n>1) will be governed by the equation:
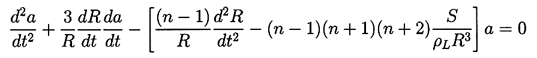 | ......(2.71)
|
|---|
The coefficients require knowledge of the global dynamic behavior, R(t).
It is clear from this equation that the most unstable
circumstances occur when dR/dt<0 and
d2R/dt2≥0.
These conditions
will be met just prior to the rebound of a collapsing cavity.
On the other hand, the most stable circumstances occur when dR/dt>0
and d2R/dt2<0, which is the case for growing
bubbles as they approach their maximum size.
The fact that the coefficients in Equation 2.71 are not constant
in time causes departure from the equivalent Rayleigh-Taylor instability
for a plane boundary.
The coefficient of a is not greatly dissimilar from the case of
the plane boundary in the sense that instability is promoted when
d2R/dt2>0 and surface tension has a
stabilizing effect.
The primary difference is caused by the da/dt term, which
can be interpreted as a geometric effect.
As the bubble grows the wavelength on the surface increases,
and hence the growth of the wave amplitude is lessened.
The reverse occurs during collapse.
Plesset and Mitchell (1956) examined the particular case of
a vapor/gas bubble initially in equilibrium that is subjected to a
step function change in the pressure at infinity.
Thermal and viscous effects are assumed to be negligible. The effect
of a fixed mass of gas in the bubble will be included in this presentation
though it was omitted by Plesset and
Mitchell. Note that this simple growth problem for a spherical bubble
was solved for R(t) in Section 2.4. One feature of that solution
that is important in this context is that
d2R/dt2≥0. It is this feature that gives rise to the instability.
However, in any real scenario, the initial acceleration phase for which
d2R/dt2≥0 is of limited duration, so the issue will be whether
or not the instability has sufficient time during the acceleration phase
for significant growth to occur.
It transpires
that it is more convenient to rewrite Equation 2.71 using
y=R/Ro as the independent variable rather than t.
Then a(y) must satisfy
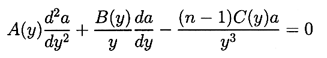 | ......(2.72)
|
|---|
where
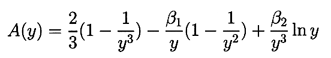 | ......(2.73)
|
|---|
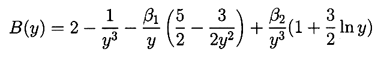 | ......(2.74)
|
|---|
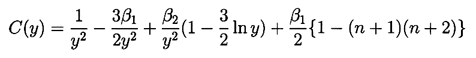 | ......(2.75)
|
|---|
and the parameters
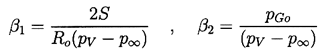 | ......(2.76)
|
|---|
represent the effects of surface tension and gas content
respectively. Note that a positive value of
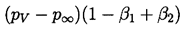 | ......(2.77)
|
|---|
implies bubble growth following t=0 whereas
a negative value implies collapse.
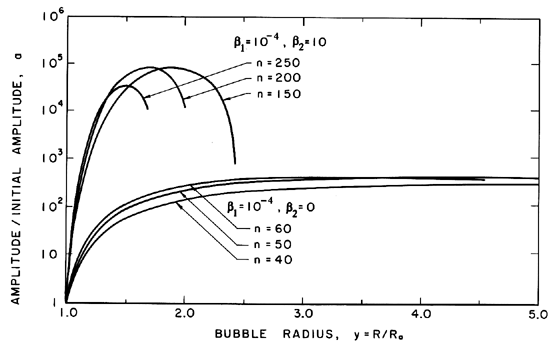
Figure 2.11
Examples of the growth of the amplitude, a,
of a spherically harmonic disturbance (of order n as indicated) on the
surface of a growing cavitation bubble for two typical choices of the
surface tension and gas content parameters, β1 and
β2.
Some typical numerical integrations of Equation 2.72
in cases of bubble growth are shown in Figure 2.11
where the amplitude scale is arbitrary.
Plesset and Mitchell performed hand calculations for small
n and found only minor amplification during growth.
However, as can be anticipated from Equation 2.72,
the amplitudes may be much larger for large n.
It can be seen from Figure 2.11 that the amplitude of the disturbance
reaches a peak and then decays during growth.
For given values of the parameters β1 and
β2, there exists
a particular spherical harmonic, n=nA, which achieves the
maximum amplitude, a; in Figure 2.11 we chose to display data
for n values which bracket nA.
The dependence of nA on β1 and
β2 is shown
in Figure 2.12.
A slightly different value of n denoted by nB gives
the maximum value of a/y.
Since the latter quantity rather than a represents a measure of
the wave amplitude to wavelength ratio, Figure 2.12 also shows
the dependence of nB on
β1 and β2.
To complete the picture, Figure 2.13 presents values of (a)max,
(a/y)max and the sizes of the bubble
(y)a=max and (y)a/y=max at which these maxima occur.
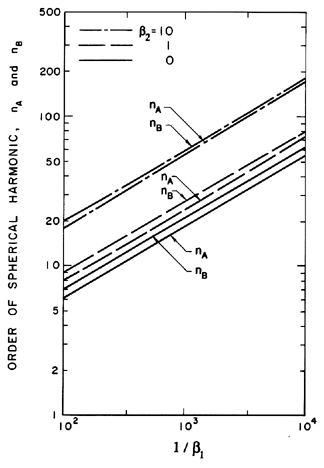
| Figure 2.12
The orders of the spherical harmonic
disturbances that, during bubble growth, produce (i) the maximum
disturbance amplitude (nA) and (ii) the maximum ratio of disturbance
amplitude to bubble radius (nB) for various surface tension and gas
content parameters, β1 and β2.
|
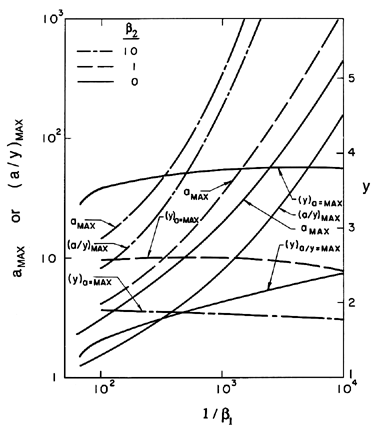
| Figure 2.13
The maximum amplification, amax, and the maximum ratio
of amplitude to bubble radius, (a/y)max, for
spherical harmonic disturbances on the surface of a growing bubble for
various surface tension and gas content parameters,
β1 and β2.
Also shown are the bubble sizes, (y)a=max and
(y)a/y=max, at which these maxima occur.
|
In summary, it can be seen that the initial acceleration phase of
bubble growth in which d2R/dt2≥0 is unstable
to spherical
harmonic perturbations of fairly high order, n. On the other hand,
visual inspection of Equation 2.71 is sufficient to conclude
that the remainder of the growth phase during which
dR/dt>0, d2R/dt2<0 is stable to all
spherical harmonic
perturbations. So, if inadequate time is available for growth of
the perturbations during the acceleration phase, then the bubble will
remain unperturbed throughout its growth. In their experiments on
underwater explosions, Reynolds and Berthoud (1981) observed bubble
surface instabilities during the acceleration phase that did correspond to
fairly large n of the order of 10. They also evaluate the duration of
the acceleration phase in their experiments and demonstrate, using an
estimated growth rate, that this phase is long enough for significant
roughening of the surface to occur. However, their bubbles become smooth
again in the second, deceleration phase of growth. The bubbles examined
by Reynolds and Berthoud were fairly large, 2.5cm to 4.5cm in radius.
A similar acceleration phase instability has not, to the author's
knowledge, been reported for the smaller bubbles typical of most
cavitation experiments. This could either be the result of
a briefer acceleration phase or the greater stabilizing effect of surface
tension in smaller bubbles.
REFERENCES
-
Birkhoff, G. (1954). Note on Taylor instability. Quart. Appl. Math.,
12, 306--309.
-
Blake, F.G. (1949). The onset of cavitation in liquids: I.
Acoustics Res. Lab., Harvard Univ., Tech. Memo. No. 12.
-
Ceccio, S.L. and Brennen, C.E. (1991). Observations of the dynamics and
acoustics of travelling bubble cavitation. J. Fluid Mech.,
233, 633--660.
-
Cha, Y.S. and Henry, R.E. (1981). Bubble growth during decompression
of a liquid. ASME J. Heat Transfer, 103, 56--60.
-
Daily, J.W. and Johnson, V.E., Jr. (1956). Turbulence and boundary
layer effects on cavitation inception from gas nuclei.
Trans. ASME, 78, 1695--1706.
-
Dergarabedian, P. (1953). The rate of growth of vapor bubbles in
superheated water. ASME J. Appl. Mech., 20, 537--545.
-
Epstein, P.S. and Plesset, M.S. (1950). On the stability of gas bubbles
in liquid-gas solutions. J. Chem. Phys., 18, 1505--1509.
-
Forster, H.K. and Zuber, N. (1954). Growth of a vapor bubble in a
superheated liquid. J. Appl. Phys., 25, No.4, 474--478.
-
Frost, D. and Sturtevant, B. (1986). Effects of ambient pressure on the
instability of a liquid boiling explosively at the superheat limit.
ASME J. Heat Transfer, 108, 418--424.
-
Fujikawa, S. and Akamatsu, T. (1980). Effects of the non-equilibrium
condensation of vapour on the pressure wave produced by the collapse
of a bubble in a liquid. J. Fluid Mech., 97, 481--512.
-
Hewitt, H.C. and Parker, J.D. (1968). Bubble growth and collapse in
liquid nitrogen. ASME J. Heat Transfer, 90, 22--26.
-
Jones, O.C. and Zuber, N. (1978). Bubble growth in variable pressure
fields. ASME J. Heat Transfer, 100, 453--459.
-
Neppiras, E.A. and Noltingk, B.E. (1951). Cavitation produced by
ultrasonics: theoretical conditions for the onset of cavitation.
Proc. Phys. Soc., London, 64B, 1032--1038.
-
Noltingk, B.E. and Neppiras, E.A. (1950). Cavitation produced by
ultrasonics.
Proc. Phys. Soc., London, 63B, 674--685.
-
Plesset, M.S. (1949). The dynamics of cavitation bubbles.
ASME J. Appl. Mech., 16, 228--231.
-
Plesset, M.S. and Zwick, S.A. (1952). A nonsteady heat diffusion problem
with spherical symmetry. J. Appl. Phys., 23, No. 1, 95--98.
-
Plesset, M.S. and Mitchell, T.P. (1956). On the stability of the
spherical shape of a vapor cavity in a liquid.
Quart. Appl. Math., 13, No. 4, 419--430.
-
Plesset, M.S. and Prosperetti, A. (1977). Bubble dynamics and cavitation.
Ann. Rev. Fluid Mech., 9, 145--185.
-
Poritsky, H. (1952). The collapse or growth of a spherical bubble or
cavity in a viscous fluid.
Proc. First Nat. Cong. in Appl. Math., 813--821.
-
Rayleigh, Lord. (1917). On the pressure developed in a liquid during
the collapse of a spherical cavity. Phil. Mag., 34, 94--98.
-
Reynolds, A.B. and Berthoud, G. (1981). Analysis of EXCOBULLE two-phase
expansion tests. Nucl. Eng. and Design, 67, 83--100.
-
Schrage, R.W. (1953). A theoretical study of interphase mass transfer.
Columbia Univ. Press.
-
Scriven, L.E. (1959). On the dynamics of phase growth. Chem. Eng.
Sci., 10, 1--13.
-
Shepherd, J.E. and Sturtevant, B. (1982). Rapid evaporation near the
superheat limit. J. Fluid Mech., 121, 379--402.
-
Theofanous, T., Biasi, L., Isbin, H.S., and Fauske, H. (1969). A
theoretical study on bubble growth in constant and time-dependent
pressure fields. Chem. Eng. Sci., 24, 885--897.
Back to table of contents
Last updated 12/1/00.
Christopher E. Brennen